For a vector v = ( m, n, p), where m, n, p are scalar functions, to be written as the gradient of a scalar function, we must have the condition ∇ × v = 0. I am asked to write an implementation of the gradient descent in python with the signature gradient (f, p0,.

Differentiation - Gradient Function Dy/Dx | Calculus By Examsolutions - Youtube
Our online calculator is able to find the gradient of almost any function, both in general form and at the specific point, with step by step solution.
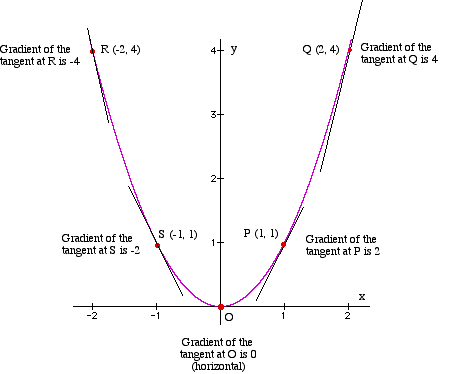
Find gradient function. In cartesian coordinates, this means. The gradient of a differentiable function contains the first derivatives of the function with respect to each variable. For a function of two.
This can help us sketch complicated functions by find turning points, points of inflection or local min or. To see this let’s start with the equation z = f (x,y) z = f ( x, y) and we want to find the tangent plane to the surface given by z = f (x,y) z = f ( x, y) at the point (x0,y0,z0) ( x 0, y 0, z 0). For detailed calculation, click “show steps”.
If we want to find the gradient at a particular point, we just. The gradient (or gradient vector field) of a scalar function f(x 1, x 2, x 3,., x n) is denoted ∇f or ∇ → f where ∇ denotes the vector differential operator, del.the notation grad f is also. Initializing all the necessary parameters and deriving the gradient function for the parabolic equation 4x 2.
You can enter the values of a vector line passing from 2 points and 3 points. The gradient can be defined as the compilation of the partial derivatives of a multivariable function, into one vector which can be plotted over a given space. Then, you can use the information given by the gradient to select the variable (s) to change.
This website uses cookies to ensure you get the best experience. Finding gradient of an unknown function at a given point in python. One of the best uses of differentiation is to find the gradient of a point along the curve.
The derivate of x 2 is 2x, so the derivative of the parabolic. The numerical gradient of a function is a way to estimate the values of the partial derivatives in each dimension using the known values of the function at certain points. You could use the following formula:
Function gradient calculator number of variables. The gradient function is a simple way of finding the slope of a function at any given point. But it's more than a mere storage device, it has several wonderful interpretations and many,.
For example, adopting a steepest descent you may apply a change proportional to the. Get the free gradient of a function widget for your website, blog, wordpress, blogger, or igoogle. By using this website, you.
Find more mathematics widgets in wolfram|alpha. Where ‘rosen’ is name of function and ‘x’ is passed as array. The gradient the gradient stores all the partial derivative information of a multivariable function.
As seen here, the gradient is useful to find the linear. This gradient calculator finds the partial derivatives of functions.
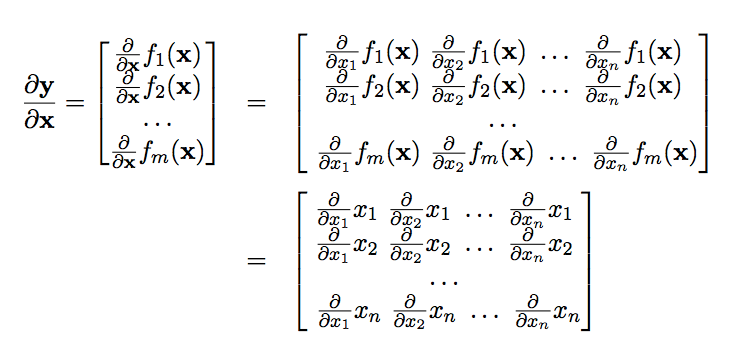
Finding The Gradient Of A Vector Function | By Chi-Feng Wang | Towards Data Science
