Three people who have scores of 52, 43, and 34 want to know how well they did on the measure. This is saying that 97.5 % of scores are outside of the shaded area on the right.
Z Scores (Z Value) & Z Table - Six Sigma Study Guide
To explain what this means in simple terms, let's use an example (if needed, see our statistical guide, normal distribution calculations , for background information on normal distribution calculations).
Units for z score. It does not use an interval scale e. As a result, you will get the final value which is 0.99266. Which of the following is unique to z scores (when compared to percentiles) a.
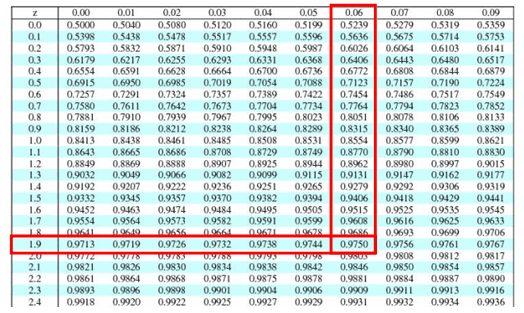
Whole number and the first digit after the decimal point). Z score and process capability are used together to get a view of your process. Then, we look up a remaining number across the table (on the top) which is 0.09 in our example.
The z score or value in process capability calculation is the mean distance from specification limits (usl and lsl) measured in standard deviation units. Zetta (unit symbol prefix z) is a decimal unit prefix in the metric system denoting a factor of 1021 or 1000000000000000000000. It is used to compare an individual data point with respect to the group c.
Remember, these percentages remain true only if our sample or population is normally distributed! In another example, a raw score of 1600 from a distribution with mean 1000 and variance 90,000 is given. For example, z = ± 2 represents the region under the probability curve that is within two standard deviations of the mean.
Here's the same formula written with symbols: It does not limit to any specific distribution. Z score tells the defects within the system.
Z = x − μ σ z = standard score x = raw observed data point μ = population mean σ = population standard deviation. It can compare scores with different units d. How do we find the z score?
What does the unit z mean? Hope that helped answer link It uses standard deviations as a metric f.
In this case it is 1.0. For z = 1.96, p =.97500 if we multiply that by 100, that means that 97.50% of the scores in this distribution will be below this score. Additionally, the area for all scores less than zero is half (50%) of the distribution.
In other words, z score tells the number of standard deviation existed between the mean and. Z = 52 − 40 7 = 1.71 z = 43 − 40 7 = 0.43 z = 34 − 40 7 = − 0.80 a problem is that these new z. Because of the symmetry, the interval from 0 to +0.65 must be half of that:
It transforms a raw score to another scale b. This tells us that an exam score of 80 is. It represents the number of standard deviations from the mean.
Standard normal distribution table) comes handy.

Z-Score: Definition, Formula, And Uses - Statistics By Jim

Z-Score: Definition, Calculation & Interpretation | Simply Psychology