If the slope of the curve y= b−xax at the point (1,1) is 2, then the values of a and b are respectively a 1,−2 b −1,2 c 1,2 d none of these hard solution verified by toppr correct. Mathematics, 21.06.2019 22:00 `if you have a set of parallel.
Differentiation From First Principles - Slope Of The Curve F(X) = X² - Youtube
In this case, we can take the derivative of y with respect to x, and plug in the desired value for x.
Slope of the curve at a point. In this video, i discuss one of the first few concepts that are learned in any calculus course: You can take whichever one you want, or even average the slopes on each side if. The slope of a function, f, at a point x = (x, f(x)) is given by m = f '(x) = f '(x) is called the derivative of f with respect to x.
Find an equation of the tangent line to the curve at \ (. The point where the curve and the tangent meet is called the point of tangency. Application of slope of tangent is temperature change at a particular time, velocity of a falling object at a particular time, current.
The slope of a curve at a point. 1 show answers another question on mathematics. The equation of the curve is a x 2=y+5 b y 2=x−5 c y 2=x+5.
Recall that the slope of the curve at a point p (x,y) is dy dx. To find the slope at a point of our function, we need to find its derivative first. This is a separable variable type.
The slope of a tangent line can be found by finding the derivative of the curve f (x and finding the value of the derivative at the point where the tangent line and the curve meet. So the slope of each normal line is the opposite reciprocal of the slope of the. The slope of a curve is a slope of a tangent line for a curve at one point.
If a curve passes through the point (1,−2) and has slope of the tangent at any point (x,y) on it as x2−2y x, then the curve also passes through the point : D y d x = d d x ( 2 x 3 8 x 2 + 1) d y d x = 6 x 2 16 x. To find the slope of a curve at a given point, we simply differentiate the equation of the curve and find.
Other names for f '(x): Using the product rule (and the chain rule within this product rule application), we have. Therefore, by what has been given, we have, dy dx = 2y.
One way of finding the slope at a given point is by finding the derivative. The slope of a curve at any point is the reciprocal of twice the ordinate at the point and it passes through the point (4,3). Each normal line is perpendicular to the tangent line drawn at the point where the normal meets the curve.
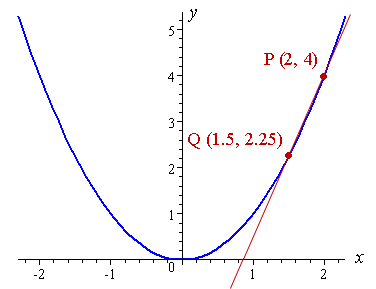
A tangent is a straight line that touches a curve at a single point and does not cross through it. Find the slope of the curve \ ( y=x^ 3+3 \) at the point \ ( p (2,11) \) by finding the limiting value of the slope of the secants through p. ⇒ dy y = 2dx.
I picked another point q to get the secant. A (3,0) b (−1,2) c (−√2,1) d (√3,0). Viewed 24k times 0 find the slope of the curve y = x 2 − 4 x − 5 at the point p ( 3, − 8) by finding the limit of the secant slopes through point p.
This will yield the equation of the tangent line to the function eqf(x)/eq at the given. 7b slope of curve 4 definition: For each point, you will have a slope to the right of the point and a slope to the left of the point.
The slope of a curve at. Curve at a particular point. To find the equation of a line, we need the slope of the line and a point on the line.
Slope of a curve the slope of a curve at a point p is de ned to be the slope of the tangent line to the curve at p.
2. The Slope Of A Tangent To A Curve (Numerical Approach)
Linear And Non Linear Relationships: Unit Three
