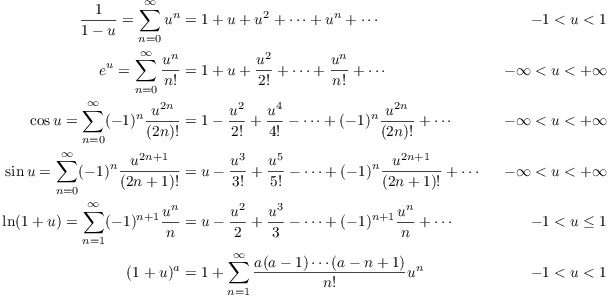Taylor series 1/(1+x) natural language; If the power/taylor series in formula (1) does indeed converge at a point x, does the series converge to what we would want it to converge to, i.e., does
Calculate the first few derivatives of f (x).

Taylor series 1-x. We see in the formula, f ( a ). The general coefficient of the expansion, for n. Thus, f (1) is the first derivative, f (2) is the second derivative, and.
The representation of taylor series reduces many mathematical proofs. This is one of the most useful maclaurin series as. For what values of x does the power (a.k.a.
This is f (x) evaluated at x = a. This will work for a much wider variety of function than the method discussed in the previous section at the expense of some often unpleasant work. In the expression above, x o is the value of x about which the series is calculated.
Calculate the first few derivatives of f ( x ). Taylor series for f (x) = 1 + x. This is f ( x) evaluated at x = a.
Taylor series 1/x centered at 1 (x x 0)n (1) converge (usually the root or ratio test helps us out with this question). Taylor series is used to evaluate the value of a whole function in each point if the functional values and derivatives are identified at a single point.
Then, we see f ' (a). Extended keyboard examples upload random. In mathematics, the binomial series is the taylor series for the function given by centered at where and.
We also derive some well known formulas for taylor series of e^x , cos(x) and sin(x) around x=0. Modified 1 year, 3 months ago. This series is used in the power flow analysis of electrical power systems.
The uses of the taylor series are: The taylor series for e x e x = 1 + x + x 2 2! 1+x+x 2 +x 3 +x 4 +…, applications of taylor series.
Using a taylor expansion to prove equality. The actual function (green) and its approximation (pink) more examples of taylor series let’s look at the function g (x) = e^x. Taylor series of $\sqrt1+x$ using sigma notation.
Derivatives derivative applications limits integrals integral applications integral approximation series ode multivariable calculus laplace transform taylor/maclaurin series fourier series. The pink line represents the approximation via an order 2 polynomial. Multivariate taylor series can be used in many optimization techniques.
In the graph below, the function 1/x is plotted around the point x=1 (left) and x=3 (right). The line in green is the actual function f (x)= 1/x. Taylor) series p 1(x) = x1 n=0 f(n)(x 0) n!
A taylor series is an expansion of some function into an infinite sum of terms, where each term has a larger exponent like x, x 2, x 3, etc. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. Viewed 93k times 7 11 $\begingroup$ i want help in writing.
We see in the taylor series general taylor formula, f (a). Ask question asked 8 years, 5 months ago. Taylor series steps step 1:
In this section we will discuss how to find the taylor/maclaurin series for a function. Here are the steps for finding the taylor series of ln (1 + x ).

Construct The Fourth Order Taylor Polynomial For F(X) = Sqrt(1+ X^2) At X = 0. Taylor Series - Youtube

Find The Taylor Series Expansion For F(X) = 1/X At X=2 - Youtube