Advertisement homerthegenius homerthegenius r = 4 sec (theta) = 4 / cos ( theta ) rectangular form: Rewrite in terms of sines and cosines.
Sec Theta = 2 To Rectangular Coordinates?? | Socratic
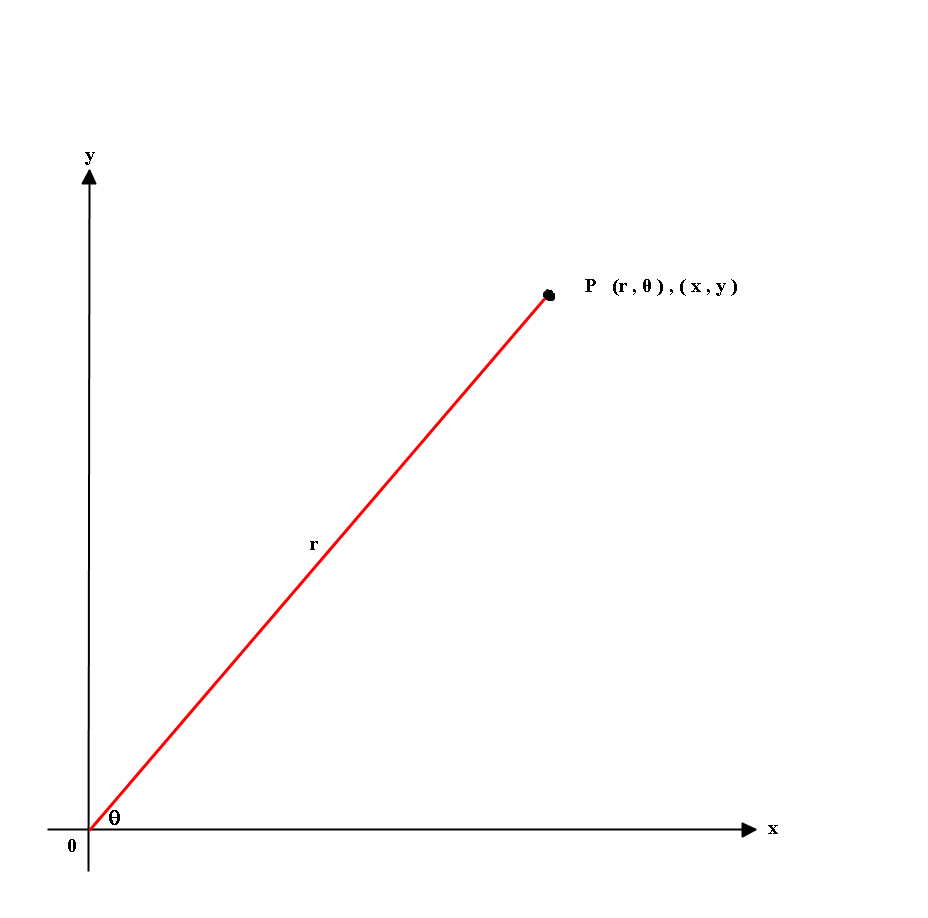
Tben, for those values of r and theta, you convert from polar coordinates to cartesian coordinates using:
R=-sec theta in rectangular form. R=tan (theta) convert to rectangular form math951 apr 9, 2016 convert form rectangular rtantheta math951 jul 2015 894 57 united states apr 9, 2016 #1 r=tan (theta) r^2=rtan (theta) x^2+y^2=r (y/x). Example 2 convert the following polar equations to their rectangular forms. It varies as a function of the angle, theta.
Convert the polar equation to rectangular form. R = 3 sec θ. R = 4 cos θ
Wis4ummerkylim wis4ummerkylim 08/07/2016 mathematics high school answered • expert verified. We cannot get rid of the r if we keep converting and squaring. Using the formulae that links polar to cartesian coordinates.
So looking at our formulas on the right, there is nothing about second tier, but we do have something that has co sign in it. We can see that the equation x = − 6 is a vertical linear function that passes through the point ( − 6, 0). First, for a given value of theta, you determine the value of r.
Convert to rectangular r=8sec(theta) step 1. R is not constant, like for a circle. Convert the polar equation to rectangular form and sketch its graph.
Make sure that the resulting rectangular equation is in its standard form. R = cos θ + sin θ r ⋅ r = r cos θ + r sin θ since r 2 = x 2 + y 2, r cos θ = x, and r sin θ = y, x 2 + y 2 = x + y step 3 is not equivalent to step 1 however, according to desmos here when zoomed in (a lot). In the case of rectangular form, we use the coordinates from the origin to get the position of the point or curve.
Change the polar equation r=5/1+cos(theta) to rectangular form. Answer x2 + y2 = 6x explanation : Use the conversion formula r(cosθ,sinθ) = (x,y).that givs r = √x2 + y2,cosθ = x r and sinθ = y r here, the conversion gives √x2 + y2 = y x or explicitly, after solving for y, y = ± x2 √1 −x2 and for real y,x ∈ ( − 1.1) not to miss is my observation that the periodicity characteristic of tanθ,θ, with period π, for θ ∈ ( − ∞,∞) in polar
So let's go ahead and rewrite this because they are reciprocal is we can write our equals negative one divided by co second data. This means that the polar form of r = − 6 sec θ is equal to x = − 6. We are going to convert our polar equation r equals negative, seeking data to rectangular.
R represents the distance and θ represents the angle. Convert r=tan(theta)*sec(theta) into cartesian, convert r=tan(theta)*sec(theta) into rectangular, convert polar equation into cartesian equations. R2 = x2 + y2 x = rcosθ ⇒ cosθ = rx then here r = 6cosθ ⇒ r = 6 × rx (multiply both sides by r) hence r2 = 6x ⇒ x2 + y2 = 6x answer verified by toppr upvote (0) was this answer helpful?
X = r*cos (theta) y = r*sin (theta) lawrence c. As as we know sector sizable toe one by cost data. The polar coordinates r and theta are related to rectangular coordinates x and y through x = r cos(theta) and y = r sin(theta) so r = sqrt(x^2 + y^2.
The given equation r = sec θ is a representation of the polar form. R is equal to pull sec tater and we need to convert it into a rectangular form so we can diet this one. Find an answer to your question convert to rectangular form r=4sec theta.
Which of the following identities should use to help her? So we will use here so he can died easily this one as after cross will delegation, we can write our cost two days equal to two. R = 3 sec θ = 3 ⋅ 1 cos θ r=3 \\text \\textsec\\text \\theta= 3 \\cdot \\frac1{\\text.
How do you convert r = 6cos(θ) to rectangular form?

Converting Equations From Polar To Rectangular - Precalculus | Socratic
How To Transform The Polar Equation R Sec Θ = 4 To An Equation In Rectangular Coordinates - Quora