D dx [sin( √ex + a 2)] not what you mean? Contents 1 examples 2 proofs

Example: Derivatives With Fractions - Youtube
The definition of the derivative is derived from the formula for the slope of a line.

Derivative of fraction. D dx (sin(x)) = lim h→0 sin(x+h) −sin(x) h d d x ( sin ( x)) = lim h → 0 sin ( x + h) − sin ( x) h since we can’t just plug in h = 0 h = 0 to evaluate the limit we will need to use the following trig. The fractional derivative of the function is given by (2) (3) (4) (5) (6) for. Decimal to fraction fraction to decimal radians to degrees degrees to radians hexadecimal scientific notation distance weight time.
Type in any function derivative to get the solution, steps and graph. Here is the definition of the derivative for the sine function. The derivative calculator supports solving first, second., fourth derivatives, as well as implicit differentiation and finding the zeros/roots.
Fractions are the numbers that represent the parts of a whole, eg. In applied mathematics and mathematical analysis, a fractional derivative is a derivative of any arbitrary order, real or complex. The derivative of a function is the rate of change of the function's output relative to its input value.
Given y = f (x), the derivative of f (x), denoted f' (x) (or df (x)/dx), is defined by the following limit: Basically, you calculate the slope of the line that goes through f at the points x and x+h. Instead, we're going to have to start with the definition of the derivative:
Here are useful rules to help you work out the derivatives of many functions (with examples below ). In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Set differentiation variable and order in options.
Wolfram|alpha calls wolfram languages's d function, which uses a table of identities much larger than one would find in a standard calculus textbook. The quotient rule is a formula for finding the derivative of a fraction. It gives the average rate of change of the function over the interval also written (the connection is that or ) but that fraction is not the derivative.
It’s only an approximation of the derivative. The derivative of f (x) is mostly denoted by f' (x) or df/dx, and it is defined as follows: In order to differentiate the exponential function.
The concept of generalized derivatives or fractional derivatives is to extend traditional derivatives such as newton's classical derivative [6] [7] [8]. There are rules we can follow to find many derivatives. Its first appearance is in a letter written to guillaume de l'hôpital by gottfried wilhelm leibniz in 1695.
Finding the derivative of a function is called differentiation. Not exactly what you’re looking for? The approximation gets better as approaches that is, as approaches
Result above, enter the function to derive. Calculus derivative calculator step 1: F (x) = a^x, f (x) = ax, we cannot use power rule as we require the exponent to be a fixed number and the base to be a variable.
Type the numerator and denominator of your problem into the boxes, then click the button. [1] [2] [3] let where both g and h are differentiable and the quotient rule states that the derivative of f(x) is it is provable in many ways by using other differential rules. Recommend this website if you like this website, then please support it by giving it a like.
The three main types of fractions are proper, improper and mixed fractions. E a x + ω sin cos tan e x ln x a a x ^ σ asin Learn properties, parts and examples of fractions at byju's.
This page will show you how to take the derivative using the quotient rule. Let f ( x) = 2 t 7 let the numerator and denominator be separate functions, so that g ( x) = 2 h ( x) = t 7 so f ( t) = g ( t) h ( t) the quotient rules states that Why is a derivative not considered a fraction?
But it can also be solved as a fraction using the quotient rule, so for reference, here is a valid method for solving it as a fraction. The slope of a constant value (like 3) is always 0 the slope of a line like 2x is 2, or 3x is 3 etc and so on. With the limit being the limit for h goes to 0.
Use the quotient rule to differentiate algebraic fractions or any other function written as quotient or fraction of two functions or expressions. You can also get a better visual and understanding of the function by using our graphing tool. The fraction is an actual quotient.
Fractional derivative download wolfram notebook the fractional derivative of of order (if it exists) can be defined in terms of the fractional integral as (1) where is an integer , where is the ceiling function. The derivative tells us the slope of a function at any point. Not exactly what you’re looking for?
Enter the function you want to find the derivative of in the editor. In this video, i work out an example of taking derivatives involving fractions (not using the quotient rule).
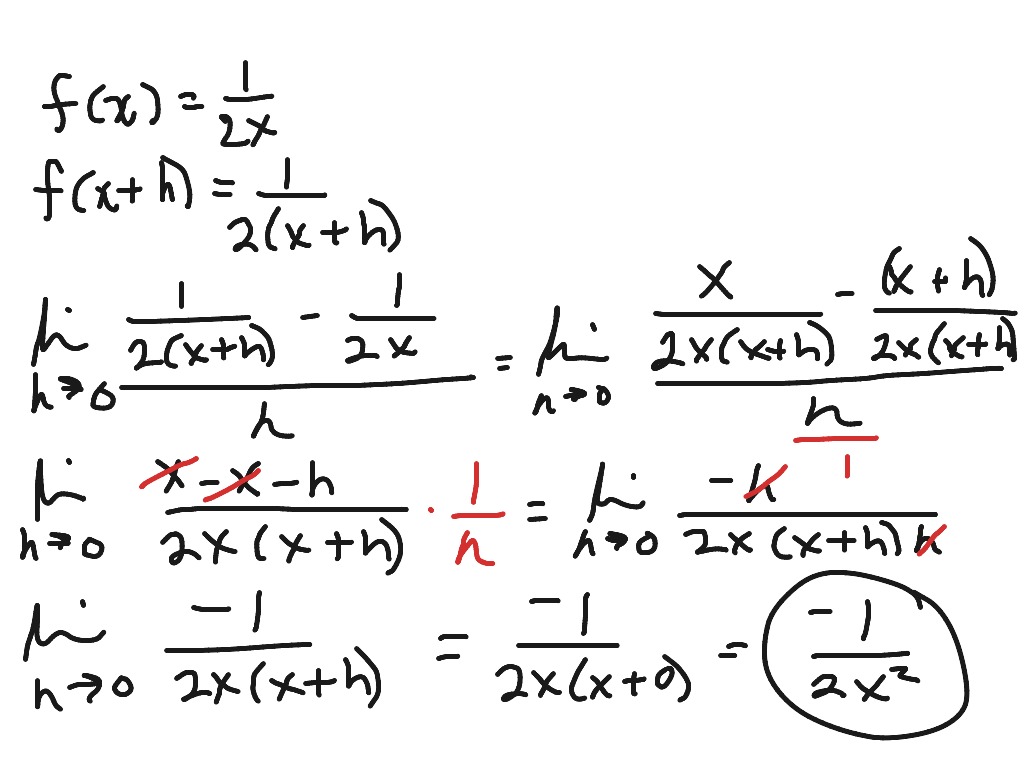
Derivative Fraction Using Limit Process | Math, Calculus | Showme

Quotient Rule Formula & Examples | What Is The Quotient Rule? - Video & Lesson Transcript | Study.com